Recursion
In this lab, we’ll explore the fundamental programming concept of recursion, a method of solving a problem where the solution depends on solutions to smaller instances of the same problem. Pieces of this lab are based on problems written by Dominique Thiebaut at Smith College, and it was adapted for this course in June 2018 by R. Jordan Crouser.
A First Look at Recursion
We’ll start with a simple example of recursion with which you are already familiar: finding the factorial of a given number:
\[n! = n*(n-1)*...*2*1\] Looking at this a little more carefully, we can see that finding the value of \(n!\) is the same as finding the value of \((n-1)!\) and then multiplying it by \(n\):
\[n! = n*\left((n-1)*...*2*1\right)=n*(n-1)!\] Similarly, \((n-1)!\) is the same as finding the value of \((n-2)!\) and then multiplying it by \((n-1)\), and so on. This is a perfect occasion to use recursion!
To see how this works in code, copy the following program into a file called factorial.py:
# factorial.py
# Demonstrates a recursive factorial function
def factorial( n ):
# stopping condition
if n<=1:
return 1
# recursive step
y = factorial(n-1)
result = n * y
return result
def main():
n = int( input( "Enter a positive number: " ) )
x = factorial(n)
print( "{0:3}! = {1:20}".format( n , x ) )
main()Now try running it. Recommendation: start with a value < 15.
Check to ensure that it returns the correct result. Here are a few values with which you can compare:
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
11! = 39916800
12! = 479001600
13! = 6227020800
14! = 87178291200 What happens if you try to run it again with 1000 as the input?
Hmm… you probably get an Exception, the end of which looks something like this:
Unfortunately, one downside of recursion is that the system has to keep track of all those intermediate results so that it can combine them in the end. To avoid letting a runaway recursive process hijack your computer, the system limits the number of recursive calls that can be made at once (the “recursion depth”).
 Challenge 1: Runtime and Recursion depth
Challenge 1: Runtime and Recursion depth
Modify the main() function in factorial.py so that instead of asking the user for input, it loops over all values from 1 to 1000 and calculates the factorial(...) for each.
Use the time module to calculate how long each call takes, and note which value finally causes a RecursionError.
Surprise, surprise… if we just ask politely, Python will tell us the maximum recursion depth without us having to guess:
Is this about the same as where your program crashed?
Multiple recursive calls
In the previous example, each partial solution built linearly on the previous one. However, there’s no requirement that this be the case!
Let’s consider another (possibly) familiar example, the Fibonacci numbers:
\[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ...\]
Do you see the pattern? Let’s write it out another way:
fibonacci(1): 1
fibonacci(2): 1
fibonacci(3): 2 = 1 + 1
fibonacci(4): 3 = 1 + 2
fibonacci(5): 5 = 2 + 3
fibonacci(6): 8 = 3 + 5
fibonacci(7): 13 = 5 + 8
fibonacci(8): 21 = 8 + 13
fibonacci(9): 34 = 13 + 21
fibonacci(10): 55 = 21 + 34
fibonacci(11): 89 = 34 + 55
fibonacci(12): 144 = 55 + 89
fibonacci(13): 233 = 89 + 144
fibonacci(14): 377 = 144 + 233
fibonacci(15): 610 = 233 + 377 Challenge 2: Recursive Fibonacci
Challenge 2: Recursive Fibonacci
Make a new file called fibonacci.py, and implement a function called fibonacci(n) that takes an integer n as input and returns the \(n^{th}\) Fibonacci number. Demonstrate that it works by calling it inside a loop in your main() function to print the first 15 Fibonacci numbers, checking above to ensure that your computation is correct.
Note: There are many ways to calculate Fibonacci numbers, but for now you should implement the fibonacci(n) function using recursion.
Recursion in Nature
Numerical calculation isn’t the one place where recursion shows up. In fact, there are numerous examples in the natural world you may already know:






These examples of visual recursion are a little bit different in that we are replicating differently-sized copies of the same thing, and arranging them in a particular way (ratehr than using their results to calculate the next step). However, the concept is the same.
Let’s have a little fun with some visual recursion of our own!
Drawing Fractals with Turtle Graphics
The turtle module provides some basic tools for drawing lines on the screen in an animated way. If you’re not familiar with the early history of computer graphics, you can read more here.

The turtle has three attributes: a location, an orientation (or direction), and a pen. The pen has attributes as well: color, width, and on/off state.
We can think of drawing a picture as telling the turtle to walk around the page, turning the pen to the on state when we want him to draw and off when we just need to reposition him. Make sense?
Here’s how the basic setup for using the turtle module (Note: don’t save this program as turtle.py; if you do, python will assume you want to import that file instead of the actual turtle module!):
import turtle
# Set things up
fred = turtle.Turtle() # We'll call him Fred, seems like a nice name
window = turtle.Screen()This isn’t particularly interesting, because we haven’t asked Fred to move anywhere and so he’s just sitting in the middle of the screen facing to the right.
Lets change that:
import turtle
# Set things up
fred = turtle.Turtle()
window = turtle.Screen()
# Draw a line 150 pixels long
fred.backward(150)Look at that, he drew a line! All he knows how to do is move forward, backward and turn left and right, but we can use that to get him to draw a circle:
import turtle
# Set things up
fred = turtle.Turtle()
window = turtle.Screen()
# Draw a circle
for i in range(360):
fred.forward(1) # Take 1 step forward
fred.right(1) # Turn 1 degree to the rightrecursion… perhaps a Koch Curve?
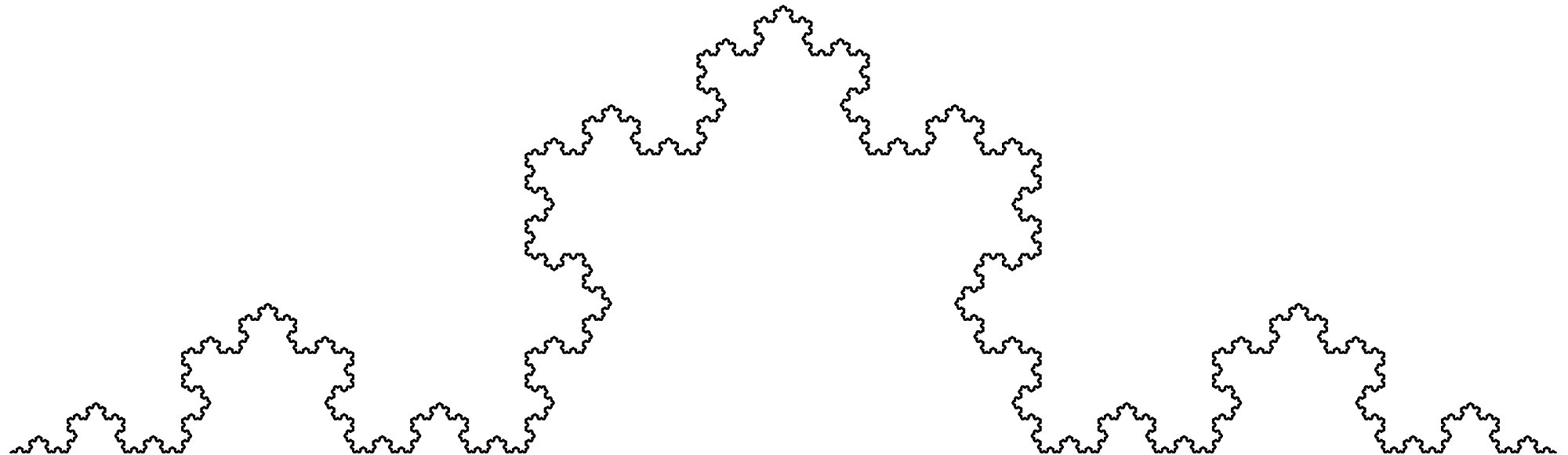
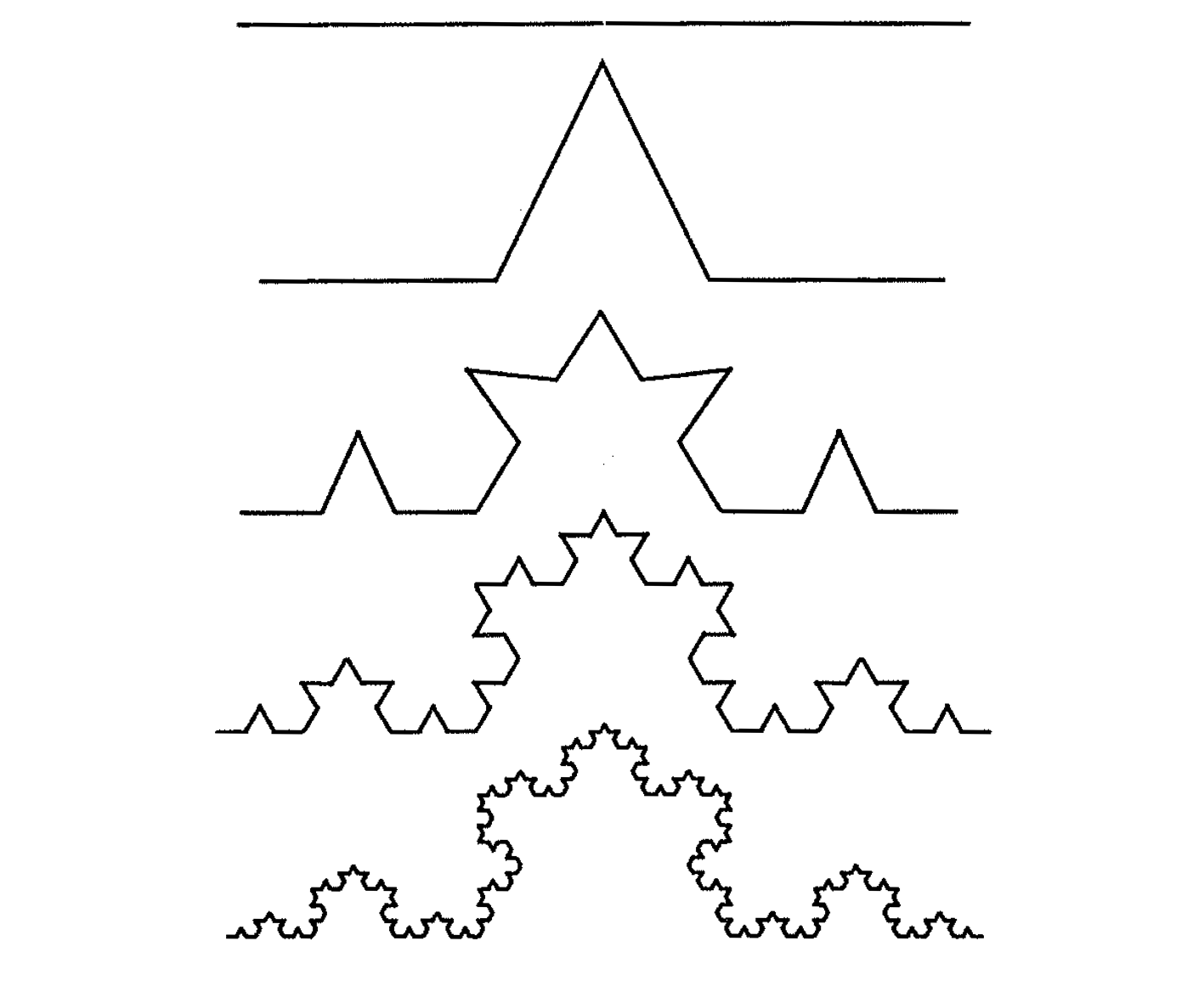
The base case is just a straight line. To draw the next level:
- Draw a line 1/3 the total length
- Rotate 60° to the left
- Draw another line 1/3 the total length
- Rotate 120° to the right
- Draw a third line 1/3 the total length
- Rotate 60° to the left
- Draw a fourth and final line 1/3 the total length
For each subsequent level, we simply take one of the “lines” and draw a shrunken copy of the procedure outlined above. Let’s code this up:
import turtle
def koch(t, order, size):
if order == 0: # The base case is just a straight line
t.forward(size)
else:
koch(t, order-1, size/3) # koch-ify the 1st line
t.left(60) # rotate 60deg to the left
koch(t, order-1, size/3) # koch-ify the 2nd line
t.right(120) # rotate 120deg to the right
koch(t, order-1, size/3) # koch-ify the 3rd line
t.left(60) # rotate 60deg to the left
koch(t, order-1, size/3) # koch-ify the 4th line
def main():
fred = turtle.Turtle()
window = turtle.Screen()
fred.color("blue")
# We'll need to move Fred over to the left to start
fred.penup()
fred.backward(150)
fred.pendown()
# Call the koch procedure to start drawing
koch(fred, 3, 300)
main()Try changing the level (the \(2^{nd}\) parameter) to a different number and see what happens!
 Final Challenge: Custom Fractals
Final Challenge: Custom Fractals
Can you figure out how to draw another kind of fractal? Some fun ones are:
The Dragon of Eve
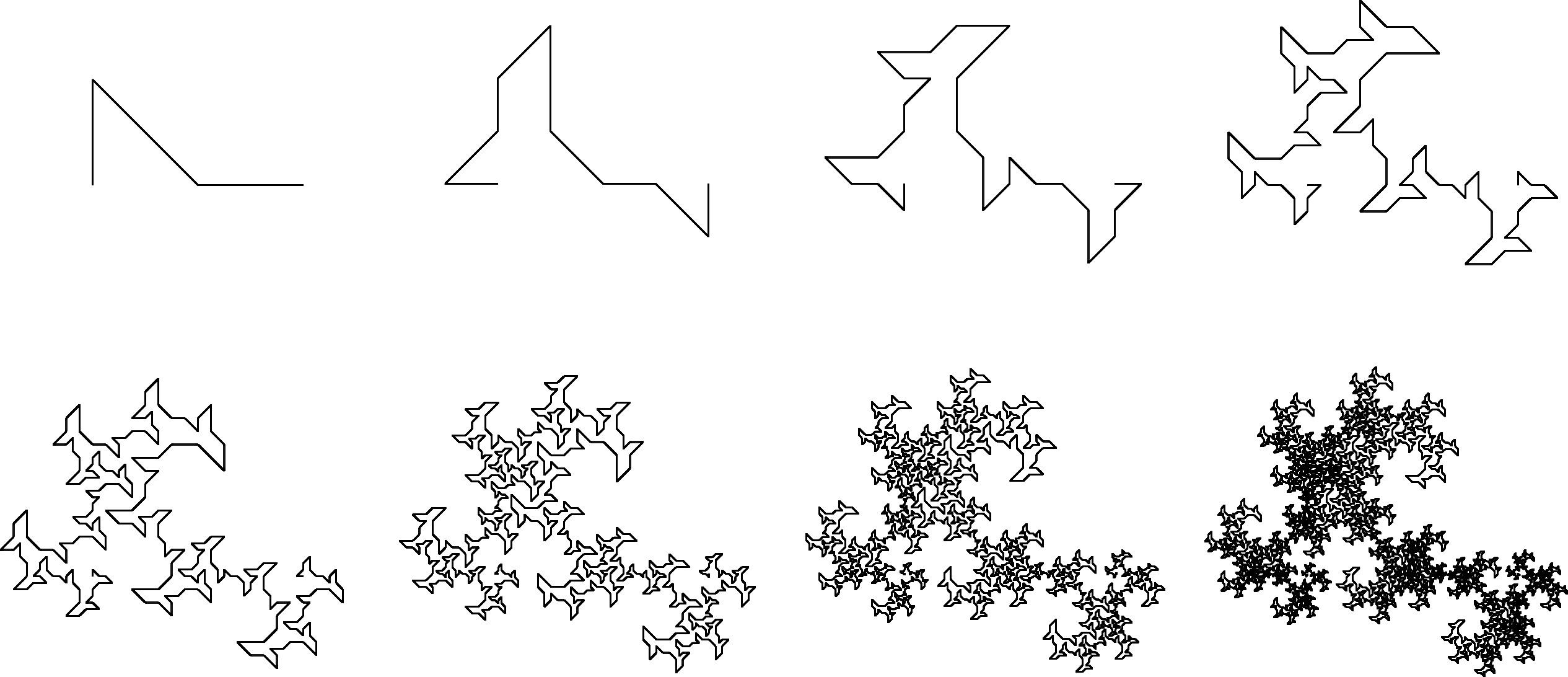
The Sierpinski Triangle

The Hilbert Curve

Try out one of these, or invent your own!
Submission of Lab 9
- Use this link to submit the link your replt.it file via Moodle.